节点插入的含义是在不改变曲线形状的前提下，向节点序列(knot vector)中插入节点。节点插入的出发点与Bezier曲线的升阶一样，都是想增加控指点的数量以增加曲线的自由度。在不考虑改变曲线阶次的情况下，根据 m=p+n+1的等式，节点数加一，控制点数量加一。

假设欲插入的节点为u,且\(u\in[u_k,u_{k+1})\),根据B样条的强凸包性，\([u_k,u_{k+1})\)段曲线由控制点\(P_{k-p},…,P_k\)控制。节点插入也仅影响这些控制点。节点插入的方式是：在\(P_kP_{k-1}\)上寻找\(Q_k\)，在\(P_{k-1}P_{k-2}\)上寻找\(Q_{k-1}\)，….，在\(P_{k-p-1}P_{k-p}\)上寻找\(Q_{k-p-1}\)。即在p+1个控制点所构成的p条边上找到p个点，连同原控制多边形的首尾\(P_k,P_{k-p}\)共p+2个点，代替原来p+1个控制点构成新曲线的控制点序列，其他控制点不变。如下图所示：

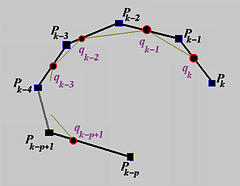
\(Q_i\)的计算公式为：$$Q_i = (1-\alpha _i)P_{i-1}+\alpha _iP_i$$ $$\alpha_i = \frac{u-u_i}{u_{i+p}-u_i} ;k-p+1\le i \le k$$这个计算模式可以用下图来表示，插入节点u所影响的控制点在左列，插入后新计算得到的控制点列在右边。连线表示\(Q_i\)是由\(P_{i-1}\),\(P_i\)线性组合构成的，系数分别为\(1-\alpha_i\)与\(\alpha_i\)。计算完成后，由蓝色虚线圈出来的点代替原来的控制点。

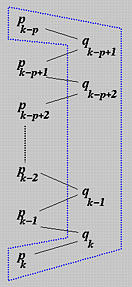
下面看一下节点插入的几何解释。\(\alpha_i:1-\alpha_i\)是节点u将区间\([u_i,u_{i+p})\)分成两部分的比例。

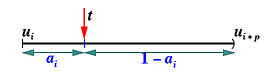
因此，如果我们把p次“切角”的\(\alpha\)都堆起来，效果如下图所示。u对每一个区间\([u_{k-p+1},u_{k+1})\),\([u_{k-p+2},u_{k+2})\),…,\([u_{k},u_{k+p})\)分隔而成的比例，成为了其控制点“切角”的比例。

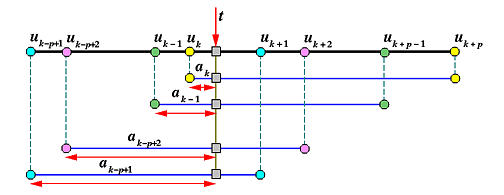
我的插入节点算法的C++实现如下:

void BSpline::InsertKnot(double u)
{
	std::vector<double>& knots = m_vecKnots;
	int p = m_nDegree;

	//查找 u 所在区间
	int k = std::distance(knots.begin(),std::upper_bound(knots.begin(), knots.end(), u))-1;
	Point *pArray = new Point[p];

	//i \in [k,k-p+1]
	//j为数组pArray位置
	for (int i = k,j=p-1;i>k-p;--i,--j)
	{
		double alpha = (u - knots[i]);
		double dev =  (knots[i + p] - knots[i]);
		alpha = (dev !=0)? alpha/dev:0;

		pArray[j] = m_vecCVs[i - 1] * (1 - alpha) + m_vecCVs[i] * alpha;
	}

	//将cv [k-p+1,k-1]替换为pArray，并且在cv[k]之前插入 pArray[p-1]
	for (int i = k - p + 1, j = 0;i < k;++i, ++j)
	{
		m_vecCVs[i] = pArray[j];
	}
	m_vecCVs.insert(m_vecCVs.begin() + k, pArray[p - 1]);

	//knots 插入u
	knots.insert(knots.begin() + k + 1, u);

	delete[] pArray;
}

下图是对某一3阶样条曲线在\(u=3000\)处进行三次插值的结果对比(插值后曲线人为移动开方便展示)：

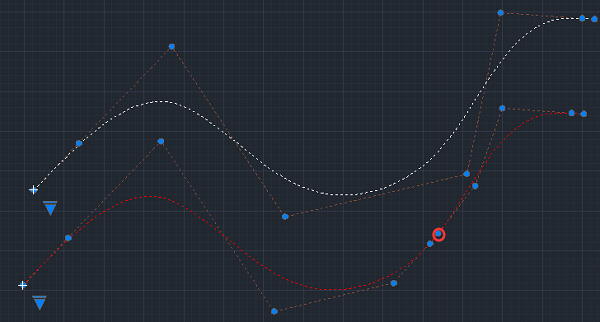
本节参考 Introduction to Computing with Geometry 6.4.1节。