贝塞尔曲线最常见的功能就是给定参数点u,计算对应曲线上的点C(u)。这个过程是正算过程，即给定参数求表达式的值。最简单的方法是根据公式，首先计算各基函数的值，然后与相应的控制点相乘，相加。但是这样会计算u的n次幂，有可能是数值不稳定的。本文介绍的德卡斯特里奥(De Casteljau’s)算法，是一种数值稳定的方法。

De Casteljau’s 算法的思想是:假设bezier曲线的控制点序列为\(P_{00},P_{01},\cdots,P_{0n}\)，确定点序列\(P_{10},P_{11},\cdots,P_{1n-1}\)，其中\(P_{ji} = uP_{j-1i} + (1-u)P_{j-1i+1}\)共n个点，然后重复迭代，直至n次迭代后，只剩下一个点，即为所求点。如下图：

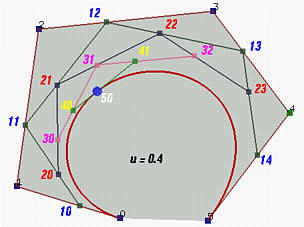
5阶bezier曲线的控制点为\(0,1,…,5\)，欲求u=0.4时的点，首先对控制多边形进行“切角”,得到5个新点\(10,11,…,14\)，经过5次切角后，得到的点50即为u=0.4时的值。

一种递归的解法：

有了迭代公式，我们就知道了算法可以通过递归实现。

Point deCasteljau(int i,int j,double u)
{
   if(0==j)
    return Pi;
   else
    return (1.0-u)*deCasteljau(i,j-1,u) + u*deCasteljau(i+1,j-1,u);
}

Point Evalute(double u)
{
   return deCasteljau(0,n,u);
}

但是你很快会发现，递归有个比较严重的问题，就是出现了大量的重复计算。他的模式与Fibonacci “肥不拿七”函数是一样的，其递归路径构成了一个有向图，而非树结构，大部分的中介节点要被重复计算若干遍。如下图：

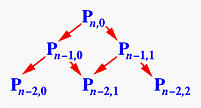
非递归解法：

按照迭代公式，首先构造一个n+1的数组A，将控制点序列\(p_0,p_1,…,p_n\)存入，然后执行n次迭代，取最后一次迭代计算出的点A[0]即为所求点。

Point Evaluate(Point A[],int n,double u)
{
	for(int i=0;i<n;++i)
	{
		for(int j=0;j<n-i;++j)
			A[j] = (1.0-u)*A[j]+u*A[j+1];
	}
	return A[0];
}

上述算法的时间复杂度为O(n),空间复杂度为O(n)。具备数值稳定的特性。

本文参考Introduction to Computing with Geometry 的第五章 Bezier Curves 的前三节。