因为n阶bezier曲线的控制点个数为固定的n+1个，如果需要通过增加控制点个数达到更灵活控制bezier曲线的目的，那么需要将bezier曲线的阶数增加，同时保持曲线的形状不发生变化。

假设n阶bezier曲线的控制点序列分别为\(P_0,P_1,…,P_n\)共n+1个，如果要将曲线升阶到n+1阶，则要产生n+2个控制点。因为曲线的形状不变，n+2个点的首点，尾点仍然是\(P_0,P_n\)。假设新的控制点序列为\(Q_0,Q_1,…,Q_n,Q_{n+1}\)，那么\(Q_0=P_0;Q_{n+1}=P_n\)余下n个点的计算公式是：$$Q_i=\frac{i}{n+1}P_{i-1}+(1-\frac{i}{n+1})P_i; i \in [1,n]$$

观察这个公式，可以看出 \(Q_i\)是线段\(P_{i-1}P_i\)上的一点，并且将线段分为\(\frac{i}{n+1}:(1-\frac{i}{n+1})\)两部分。这个方法与德卡斯特里奥(De Casteljau’s)算法非常相近，都是对原始控制点进行“切角”。不过，德氏算法每次切角都按照固定的比例u切割，升阶算法的比例却是与i相关的。

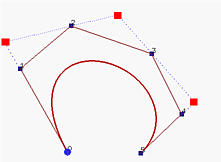
如上图，为四阶bezier曲线升阶到5阶后的效果。红色点为原始点，蓝色点为升阶后的新控制点，可见新控制点为对原始控制点进行定比分点后生成的。值得注意的是，通过“切角”运算，新的控制点总是离bezier曲线更近。

下面给出计算升阶后的新控制点的程序

/*!
*\brief bezier曲线升阶
*\ param const std::vector<Point> & control_vertex 原始控制点
*\ param std::vector<Point> & new_control_vertex 升阶后的控制点
*\ Returns:   void
*/
void Bezier::DegreeElevation(const std::vector<Point>& control_vertex,std::vector<Point>& new_control_vertex)
{
	int n = control_vertex.size();
	new_control_vertex.resize(n+1);

	new_control_vertex.front() = control_vertex.front();
	new_control_vertex.back() = control_vertex.back();

	for (int i=1;i<n;++i)
	{
		double ratio = ((double)i)/n;
		new_control_vertex[i] = ratio*control_vertex[i-1] + (1.0-ratio)*control_vertex[i];
	}
}

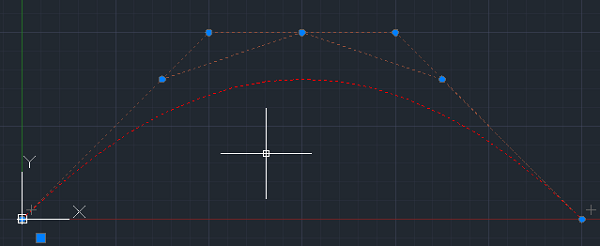
下图是3阶Bezier曲线升阶到4阶后在AutoCAD中的展现。可以看见，除了首尾控制点外，新曲线的控制点均在原始曲线的控制多边形上。

本文参考Introduction to Computing with Geometry 第五章第七节。