曲线拟合包含两个方面,插值(interpolation)和逼近(approximation)。用于曲线拟合的离散点通常不具有非常高的精度,直接插值得到的曲线可能不满足“光顺(fair)”要求,本节的目标是介绍光顺的定义,以及给出一种满足“光顺”要求的最小二乘逼近方法。
1)光顺的定义
曲线光顺其实是NURBS曲线研究的一支非常重要的分支,作为一个非数学专业的学生,我们不能完全给出非常严谨的数学定义,仅能从应用方面介绍光顺的意义及应用。首先,我已经介绍了曲线的插值是令样条曲线严格的穿过所有的型值点(Fit Point),这样求出来的曲线,因为给定点的精度问题,通常具有曲率变化幅度特别大的问题。比如下图,虚线表示秋曲线的“曲率伴随曲线”,可以看到,曲线的曲率变化是非常剧烈的(但是,曲线的曲率仍然是连续的,不要混淆),这种现象,称之为曲线不光顺。

Poliakoff J F, Wong Y K, Thomas P D. An automated curve fairing algorithm for cubic B -spline curves[J]. Journal of Computational & Applied Mathematics, 1999, 102(1):73-85.
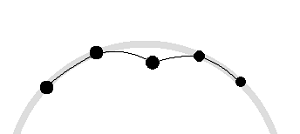
假设样条曲线是一条钢丝(就像最早的造船业使用的样条一样),被上面的四个黑色的“duck”约束,中间的黑点部分就产生了多余的弹性势能,因此,广泛的曲线“光顺”的定义就是曲线上没有多余的“能量”。
2)曲线最小二乘拟合的一般形式
因为曲线光顺优化是NURBS的一个重要的研究分支(至今仍然活跃),因此光顺算法也不一而足。其中,广泛应用的一种线性最小二乘拟合的方式一般是这样的:
最小二乘的目标函数由两部分构成,一部分为逼近项,约束曲线上的点与给定的型值点的距离不能太大。一部分为光顺项,或者称优化项,约束曲线达到“光顺要求”。目标函数的形式是:$$f=\alpha(fairing\_component)^2 + \beta(approximating\_component)^2$$两个项都是控制点P的函数,因此通过对目标函数求最小值的方式,可以计算出控制点P。至于系数\(\alpha,\beta\),属于光顺项与逼近项的权重,一般会通过实验事先确定。
在各种方法里,逼近项的形式一般是确定的,给定点\(\{F_1,…,F_x\}\),通过参数化确定他们的参数\(\{u_1,…,u_x\}\),对应曲线上的点为\(MP\),M为对应的基函数矩阵,P为控制点向量。那么逼近项则是$$MP-F=
\begin{bmatrix}
N_0(u_1)&\cdots&N_n(u_1)\\
\vdots&\ddots&\vdots\\
N_0(u_x)&\cdots&N_n(u_x)
\end{bmatrix}
\begin{bmatrix}
P_1\\\vdots\\P_n
\end{bmatrix}-
\begin{bmatrix}
F_1\\\vdots\\F_x
\end{bmatrix}$$
3)光顺项:B样条二次导数的积分的计算
至于光顺项,则有很多不同的实现方法,这里介绍一种 常见的方法:令曲线在给定点\(C(u_i)\)上二阶导数的平方和的积分最小的方法:$$\int_{t=0}^m(\sum_{j=0}^n N_{j,p}^{\prime\prime}
(u)P_j)^2du\rightarrow min$$为简化表达,令\(
W=\int_{t=0}^m(\sum_{j=0}^n N_{j,p}^{\prime\prime}
(u)P_j)^2du\),可以得出曲线拟合的目标函数\(f\)的形式为:$$f=\alpha P^TWP+\beta(MP-F)^2$$按照最小二乘法的解法:$$\frac{\partial f}{\partial P}=
2\alpha P^T(W)+2\beta(MP-F)^TM=0$$整理一下,得到$$P^T(\alpha(W)+\beta(M^TM))=\beta F^TM$$两边同时取转置,可以得到P的解:$$P=\beta(\alpha(W)+\beta(M^TM))^{-1}M^TF$$矩阵M,我已经在B样条的内插一节中涉及,这里不再赘述。比较复杂的,就是拼装矩阵W。
因为B样条的基函数\(N_{i,p}\)在区间\([u_i,u_{i+p+1}\)上非零,并且对于每一个区间\([u_k,u_{k+1})\),基函数都是关于u的三次多项式函数,那么其二次导数的形式为\(au+b\),因此我们需要求出每个区间上的a,b的值。
关于W矩阵的构造,可以构造一个n个基函数\(\times\)n+p个矩阵的辅助矩阵N,其中\(N(i,j)\)代表基函数导数\(N_{i,p}^{\prime\prime}\)在区间\([u_k,u_{k+1})\)上的多项式\(au+b\)的系数a,b。\(W_{i,j}\)的内容就是N第i行与第j行所有系数相乘后积分的结果:
$$W_{i,j}=\sum_{k=0}^{k+p}\int_{u_k}^{u_{k+1}}(N_{i,k}.a u+N_{i,k}.b)(N_{j,k}.a u+N_{j,k}.b)du$$
B样条基函数的二阶导数的递推形式如下:$$N_{i,p}^{\prime\prime}=p\cdot(p-1)\cdot\{
\frac{N_{i,p-2}}{(u_{i+p-1}-u_i)(u_{i+p}-u_i)}-
N_{i+1,p-2}\cdot(\frac{1}{(u_{i+p}-u_i)(u_{i+p}-u_{i+1})}+\frac{1}{(u_{i+p}-u_{i+1})(u_{i+p+1}-u_{i+1})})+\\
\frac{N_{i+2,p-2}}{(u_{i+p+1}-u_{i+1})(u_{i+p+1}-u_{i+2})}
\}$$
$$=c_1\frac{u-u_i}{u_{i+p-2}-u_i}N_{i,p-3}+
[c_1\frac{u_{i+p-1}-u}{u_{i+p-1}-u_{i+1}}+
c_2\frac{u-u_{i+1}}{u_{i+p-1}-u_{i+1}}]N_{i+1,p-3}+\\
[c_2\frac{u_{i+p}-u}{u_{i+p}-u_{i+2}}+
c_3\frac{u-u_{i+2}}{u_{i+p}-u_{i+2}}]N_{i+2,p-3}+
c_3\frac{u_{i+p+1}-u}{u_{i+p+1}-u_{i+3}}N_{i+3,p-3}
$$
其中c_1,c_2,c_3分别对应上面的常数项。
这篇文章里,我仍然以最常用的三阶B样条曲线的拟合为例。所以对后面的式子里,\(p=3\),如果读者想要更改曲线阶次,需要对我特别针对三次曲线所做的说明进行调整。
当p=3时,\(N_{i,p}\)在区间\([u_i,u_{i+1}),[u_{i+1},u_{i+2}),[u_{i+2},u_{i+3}),[u_{i+3},u_{i+4})\)上对应的a,b的值与二阶导数展开在\(N_{i,p-3},N_{i+1,p-3},N_{i+2,p-3},N_{i+3,p-3}\)的系数一一对应。
当计算出每个区间上的a,b值后,就可以求出W矩阵了。自此,曲线整体光顺逼近算法就介绍完了。通过我的C++实现,可以看到具体的效果。
4)光顺效果
因为实现的代码较长,我们先看效果,把代码实现放到最后。
\(\alpha\)是光顺项的权重,\(\beta\)是逼近项的权重,通过调整两者的比例,可以使曲线获得不同的逼近效果。下图是\(\alpha=0.01,\beta=1\)时逼近曲线与插值曲线的曲率的对比,可见二者值域差别不大,逼近曲线的曲率变化稍微连续一点。二者几何差距不大。
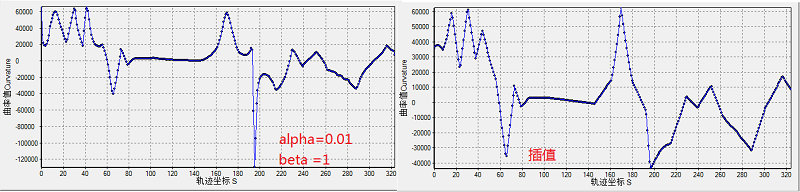
显示曲率软件copyright navinfo
下图是增大光顺项权重\(\alpha=1,beta=1\)是逼近曲线的曲率与几何(红线为逼近曲线,青线为拟合曲线)的效果:
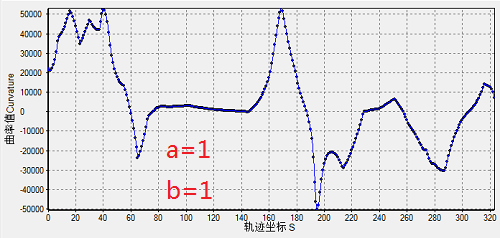
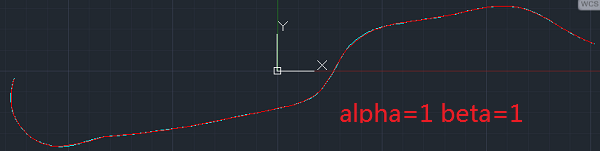
可见,增大光顺项权重后,曲线的曲率变化更加连续了,更符合“光顺”的效果了。下图是继续加大光顺处理效果\(\alpha=1,\beta=0.01\)的曲率与几何效果。可见,逼近曲线自动的平滑了弯曲较大的部分,从而趋近于减小能量。
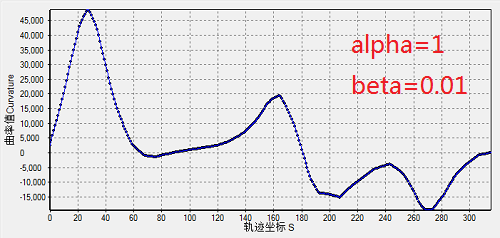
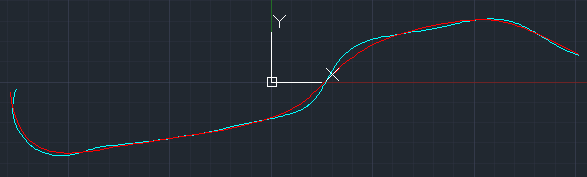
5)二次型的求导
本节相对于之前的线性的矩阵计算,又引入了矩阵求导,尤其是二次型求导部分,所以,特地将引用的二次型求导公式列举如下:$$\frac{\partial(x^TAx)}{\partial x}=x^T(A+A^T)\\
\frac{\partial(x^TAx)}{\partial z}=x^T(A+A^T)\frac{\partial x}{\partial z}$$
5)我的C++实现
#include <Dense> //Eigen
/*!
*\brief 三次B样条整体光顺逼近
*\ param const std::vector<Point> & vecFitPoints 型值点
*\ param double alpha 光顺项权重
*\ param double beta 逼近项权重
*\ Returns: BSpline 逼近结果
*/
BSpline BSpline::CubicApproximate(const std::vector<Point>& vecFitPoints,double alpha,double beta)
{
const int p =3;
BSpline bs;
int x = vecFitPoints.size();
if(x<p)
{
cout<<"too less point !"<<endl;
return bs;
}
//需要的矩阵
Eigen::MatrixXd W= Eigen::MatrixXd::Zero(x+2,x+2);
Eigen::MatrixXd P= Eigen::MatrixXd::Zero(x+2,3);
Eigen::MatrixXd M= Eigen::MatrixXd::Zero(x+2,x+2);
Eigen::MatrixXd F= Eigen::MatrixXd::Zero(x+2,3);
//参数化
bs.m_nDegree = p;
bs.m_vecKnots.resize(x); //x+6个节点
//计算节点
bs.m_vecKnots[0] =0.0;
for (int i=1;i<x;++i)
{
bs.m_vecKnots[i] = bs.m_vecKnots[i-1]
+ sqrt(PointDistance(vecFitPoints[i],vecFitPoints[i-1]));
}
//节点首尾构成p+1度重复
bs.m_vecKnots.insert(bs.m_vecKnots.begin(),p,bs.m_vecKnots.front());
bs.m_vecKnots.insert(bs.m_vecKnots.end(),p,bs.m_vecKnots.back());
//W 矩阵
WMatrix(W,x+2,p,bs.m_vecKnots);
//M矩阵
std::vector<double> basis_func;
M(0,0) = 1;
M(x-1,x+1) = 1;
for (int i=p+1;i<x+p-1;++i)
{
//c(u)在 N_{i-p},...,N_i等p+1个基函数上非零
bs.BasisFunc(bs.m_vecKnots[i],i,basis_func);
for (int j=i-p,k=0;j<=i;++j,++k)
{
M(i-p,j) = basis_func[k];
}
}
//导数
M(x,0) = -1;
M(x,1) = 1;
M(x+1,x) = -1;
M(x+1,x+1) = 1;
//F矩阵
for (int i=0;i<x;++i)
{
F(i,0) = vecFitPoints[i].x;
F(i,1) = vecFitPoints[i].y;
F(i,2) = vecFitPoints[i].z;
}
{
Vec3d v0,v1,v2;
BesselTanget(vecFitPoints[0],vecFitPoints[1],vecFitPoints[2],v0,v1,v2);
Vec3d v= v0*(bs.m_vecKnots[p+1]-bs.m_vecKnots[1])/(double)p;
F(x,0) = v.x;
F(x,1) = v.y;
F(x,2) = v.z;
}
{
Vec3d v0,v1,v2;
BesselTanget(vecFitPoints[x-3],vecFitPoints[x-2],vecFitPoints[x-1],v0,v1,v2);
Vec3d v= v2*(bs.m_vecKnots[x+1+p]-bs.m_vecKnots[x+1])/(double)p;
F(x+1,0) = v.x;
F(x+1,1) = v.y;
F(x+1,2) = v.z;
}
//解方程
P = (alpha*W+beta*M.transpose()*M).colPivHouseholderQr().solve(beta*M.transpose()*F);
#ifdef _DEBUG
cout<<"P------------------"<<endl<<P<<endl;
#endif
//将 P的值赋给 B样条
bs.m_vecCVs.resize(x+2);
for(int i=0;i<x+2;++i)
{
Point& cv = bs.m_vecCVs[i];
cv.x = P(i,0);
cv.y = P(i,1);
cv.z = P(i,2);
}
return bs;
}
void BSpline::WMatrix(Eigen::MatrixXd& W,int n,int p,const std::vector<double>& u)
{
std::vector<std::vector<std::pair<double,double>>> BasisFuncByKnot(n);
//初始化
for (int i=0;i<n;++i)
{
BasisFuncByKnot[i].resize(n+p);
for(int j=0;j<n+p;++j)
{
BasisFuncByKnot[i][j].first =0;
BasisFuncByKnot[i][j].second =0;
}
}
std::vector<std::pair<double,double>> a_b_array;
for (int i=0;i<n;++i)
{
_SecondDerivativeCoefficient(i,u,a_b_array);
std::copy(a_b_array.begin(),a_b_array.end(),BasisFuncByKnot[i].begin()+i);
}
//基函数//其实这是一个对称矩阵,我为了方便,多算了一倍
for (int i=0;i<n;++i)
{
for (int j=0;j<n;++j)
{
double ret =0;
//区间
for (int k=0;k<n+p;++k)
{
const std::pair<double,double> basis_i = BasisFuncByKnot[i][k];
const std::pair<double,double> basis_j = BasisFuncByKnot[j][k];
ret +=PolynomialIntegral(basis_i.first * basis_j.first,basis_i.first*basis_j.second+
basis_i.second*basis_j.first,basis_i.second*basis_j.second,u[k],u[k+1]);
}
W(i,j) = ret;
}
}
}
void BSpline::_SecondDerivativeCoefficient(int i,const std::vector<double>& u,std::vector<std::pair<double,double>>& a_b_array)
{
const int p = 3;
double c1,c2,c3;
c1=c2=c3=0;
double div =(u[i+p-1]-u[i])*(u[i+p]-u[i]);
if(div !=0)c1=p*(p-1)/div;
div=(u[i+p]-u[i])*(u[i+p]-u[i+1]);
if(div !=0)c2-=p*(p-1)/div;
div=(u[i+p]-u[i+1])*(u[i+p+1]-u[i+1]);
if(div !=0)c2-=p*(p-1)/div;
div = (u[i+p+1]-u[i+1])*(u[i+p+1]-u[i+2]);
if(div !=0)c3 =p*(p-1)/div;
a_b_array.resize(p+1);
for (int i=0;i<p+1;++i)
{
a_b_array[i].first =0;
a_b_array[i].second =0;
}
div = u[i+p-2]-u[i];
if(c1!=0&&div!=0)
{
a_b_array[0].first = c1/div;
a_b_array[0].second = -c1*u[i]/div;
}
div =u[i+p-1]-u[i+1];
if(div !=0)
{
a_b_array[1].first = (c2-c1)/div;
a_b_array[1].second = (c1*u[i+p-1]-c2*u[i+1])/div;
}
div =u[i+p]-u[i+2];
if(div !=0)
{
a_b_array[2].first = (c3-c2)/div;
a_b_array[2].second = (c2*u[i+p]-c3*u[i+2])/div;
}
div =u[i+p+1]-u[i+3];
if(c3!=0&&div!=0)
{
a_b_array[3].first = -c3/div;
a_b_array[3].second = u[i+p+1]*c3/div;
}
}
double BSpline::PolynomialIntegral(double quad,double linear,double con,double start,double end)
{
if(end == start)
return 0;
double ret =0;
if(quad !=0)
{
ret +=(end*end*end - start*start*start )*quad/3;
}
if(linear !=0)
{
ret +=(end*end -start*start)*linear/2;
}
if(con !=0)
{
ret +=(end-start)*con;
}
return ret;
}
参考文献:
罗卫兰. B样条曲线的光顺[D]. 浙江大学, 2003.
兰浩. NURBS曲线整体光顺逼近算法研究与应用[D]. 西安理工大学, 2008.

看过后非常有启发, 请问可以分享完整的cpp工程吗? 这里的一些数据结构没有定义.
后续应该会整理发布到github上,因为眼下工作比较紧张,排期还没有确定。
现在是2020年7月了。
能公开下基函数矩阵代码吗?BasisFunc
您好!不知道您后续是否公开了项目代码,如公开了能否提供一下公开地址呢,万分感谢您!