本系列的主题是“NURBS”，但是大部分篇幅集中与Bezier(B Spline的特殊形式)，B Spline。之所以这么安排，是因为NURBS与B样条可以轻松的互相转换，B样条的计算方法，均可以应用到NURBS(非均匀有理B样条)上。

1）提出NURBS的动机

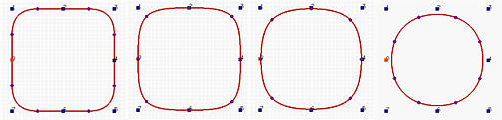
我们之前已经提到，B样条是分段的多项式函数。在设计上，B样条的应用十分广泛，但是，B样条却不能表达所有的曲线类型，比如说圆、椭圆、双曲线等。如下图，从左至右是利用阶数为2,3,510次B样条曲线拟合圆的效果，可以看到，随着曲线阶次增高，曲线越来越“圆”，但是即使是10次曲线仍然不能精确的表达圆。为了表达这些曲线类型，需要将无理B样条曲线扩展到有理B样条曲线的形式。

2）定义

将B样条的控制点P写成齐次坐标(homogeneous coordinates)形式：

$$P_i^w= \begin{bmatrix} w_ix_i\\ w_iy_i\\ w_iz_i\\ w_i \end{bmatrix}$$ B样条的定义就是 $$C(u)=\sum_{i=0}^nN_{i,p}P_i=\begin{bmatrix} \sum w_iN_{i,p}x_i\\ \sum w_iN_{i,p}y_i\\ \sum w_iN_{i,p}z_i\\ \sum w_iN_{i,p} \end{bmatrix}$$ 将齐次坐标转换为笛卡尔坐标，就是讲上述表达式的4个坐标同时除以第四维坐标： $$C(u)= \frac{1}{\sum_{i=0}^nw_iN_{i,p}}\sum_{i=0}^nN_{i,p}w_i \begin{bmatrix} x_i\\ y_i\\ z_i\\ 1 \end{bmatrix}= \frac{1}{\sum_{i=0}^nw_iN_{i,p}}\sum_{i=0}^nN_{i,p}w_iP_i$$ 就是NURBS(Non Uniform Relational B Spline 非均匀有理B样条)的定义。

相对于B样条，Nurb每个控制点均有对应的权重$w_i$。一般情况下，$w_i$为正数，当权重为0的时候，控制点$P_i$对曲线的形状完全没有影响，这个控制点称为“infinite”控制点，有特殊的应用。而且，可以观察到，NURBS的定义为有理曲线(两个关于u的p次多项式的商的形式)形式。

3）NURBS与B样条的相互转换

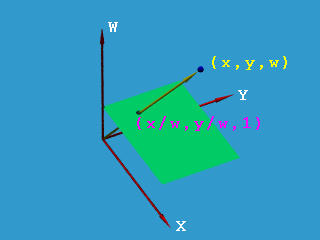
从B样条引入NURBS的定义，我们能够得出一个非常重要的结论，如果将控制点齐次坐标$[w_ix_i,w_iy_i,w_iz_i,w_i]^T$视为四维坐标，那么三维空间中的NURBS上的一个点$C(u)$,其实是四维空间中控制点序列$\begin{bmatrix}w_iP_i\\w_i\end{bmatrix}$构成的B样条在w=1上的投影。下图是几何解释，可见$(x,y,w)$在$w=1$平面上的投影为$(\frac{x}{w},\frac{y}{w},1)$。

总结一下：

• 由$w_iP_i$定义的NURBS曲线为四维控制点 $\begin{bmatrix}w_iP_i\\w_i\end{bmatrix}$定义的B样条在$w=1$上的投影。
• 当所有控制点的权重均为1时，$\sum N_{i,p}w_i=\sum N_{i,p} =1$(B样条基函数的性质)，$\frac{1}{\sum_{i=0}^nw_iN_{i,p}}\sum_{i=0}^nN_{i,p}w_iP_i=\sum_{i=0}^nN_{i,p}P_i$，也就是说，B样条是权重均为1的NURBS。

4）NURBS曲线的性质

作为B样条的一般形式，NURBS与B样条的大部分性质都是相同的。不同之处在于透视变换的不变性。B样条仅支持仿射变换的不变性，NURBS更是增加了对透视变换的不变性，这使得NURBS在计算机图形、视觉、动画方面的应用及其广泛：人眼的视角观察到的目标都是经过透视变换的。当然，透视变换改变了权重。关于透视变换与仿射变换。可以参考Dr.shene的课件Geometric Transforms。

5）NURBS曲线的计算

根据NURBS的定义，我们可以将NURBS曲线看做四维B样条在$w=1$上的投影，因此，所有针对NURBS的计算（正算，不讨论插值、拟合等问题），都可以用三步解决：

构造控制点为$\begin{bmatrix}w_iP_i\\w_i\end{bmatrix}$的四维B样条。

在四维B样条上进行计算，如求值、求导数、打断等等，得到结果(四维)。

将结果投影到$w=1$上，即前三维除以第四维，得到三维坐标，即是NURBS所求点。

6）修改权重

观察NURBS曲线的的基函数：

$$R_{i,p}=\frac{N_{i,p}w_i}{\sum_{j=0}^nN_{j,p}w_j}$$ 可以看出来，如果增加$w_i$的值，那么$R_{i,p}$的值一定会增加，所以，曲线会更向控制单$P_i$靠拢。反之，如果减小$w_i$的值，那么曲线会更加疏离控制点$P_i$。为了定量的观察，可以指定控制点$P_k$的情况：

$$C(u) = \frac{N_{k,p}w_kP_k+\sum_{i\neq k}^nN_{i,p}w_iP_i} {N_{k,p}w_k+\sum_{i\neq k}^nN_{i,p}w_i}$$ 为了简化表达，令： $$A=N_{k,p}w_k \\ B=\sum_{i\neq k}^nN_{i,p}w_i\\ X=\sum_{i\neq k}^nN_{i,p}w_iP_i$$ 原式变为 $$C(u)=\frac{AP_k+X}{A+B}$$

假设当$w=0$时的曲线为$C^0(u)$那么$w\neq 0$时的曲线的相比$C^0(u)$的位移为：

$$C(u)-C^0(u)=\frac{AP_k+X}{A+B}-\frac{X}{B}= \frac{A}{A+B}(P_k-\frac{X}{B})= \frac{A}{A+B}(P_k-C^0(u))$$ 这也佐证了当w增大时，曲线远离原曲线而更靠近控制点，而且，可以看到，曲线的位移向量与原曲线上点$C^0(u)$到控制点$P_k$的向量同方向，并且模长为后者的$\frac{A}{A+B}$倍。

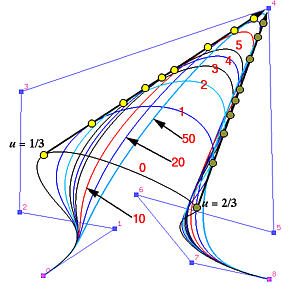
对照上图，当$w_4=0$时，对应的曲线为黑色线(红字标识0)，当$w_4$依次从1,2,3,4,5,10,20到50增长时，分别用不同颜色的线绘制出对应的NURBS曲线。可以观察到：

1）当权重不断增大时，曲线越来越向控制点$P_4$靠拢。

2）对于不同的w,观察同一点$C(u=\frac{1}{3})$与$C(u=\frac{2}{3})$(左右两侧的黄色点)，他们均在$C^0(\frac{1}{3})$与$P_4$、$C^0(\frac{2}{3})$与$P_4$的连线上。

---

参考文档：

Introduction to Computing with Geometry 7.1~7.5节