叠置分析的核心任务是解决由多个图层生成的新数据中,每个新生成的对象是由哪些输入对象“叠置”生成出来的问题。即所谓的对象标记。栅格叠置分析的标记非常简单,矢量对象的对象标记算法相对来说就要复杂很多。接上文,当输入要素建立了对象模型与拓扑模型的关联,构建拓扑模型后,本文介绍一种拓扑面标记算法,以解决叠置分析结果的标记问题。
1.输入数据
1)同一图层要素相互不压盖。 叠置分析的输入为多个专题“图层”数据。每一个区域(对应图层中的一个要素)对应一种特定的专题属性,比如在省级行政区划图中,一个区域属于山西,则不会属于河北或者其他省份。因此,输入数据的特征之一是,同一个图层内,要素不存在相互压盖的情况,对应的结果数据上,至多只对应一种要素的同一个ID。
2)多个图层的叠置分析最终会分解为多组两个图层之间的叠置分析。好比\(A\cap B\cap C\ = A\cap (B\cap C)\)一样,叠置分析(运算)满足结合律等计算规律,使得多个图层的叠置分析最终会被分解为两个图层之间的叠置。当然,这不是意味着多个图层之间的叠置是完全的两两叠置构成的,这样会造成计算效率的极大降低,而是,我后面提到的面标记算法是建立在两两图层基础上的。我们在设计算法的时候,也可以只考虑二个图层的情况。
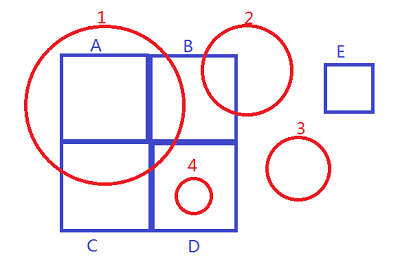
以下图作为例子引入我们的问题,两个图层分别为图层r(red),图层b(blue)。
2.拓扑模型
叠置分析首先将red blue两个图层构建拓扑,及将两个图层的几何要素构建成为DCEL描述的图结构。在geos中,这个结构称为planargraph 平面图。所有的线要素在相交处打断,并且按照规则构成拓扑面。
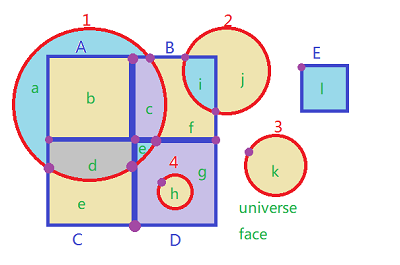
上图中构成各拓扑面(以绿色小写字母标识)的有向边并未标出。顺便说一下,这里用了四种颜色对上述图形信息填充,这是在图论里有名的“四色填图”,只用四种颜色,就可以给复杂的镶嵌图进行填色。
可以看到 对象1 构成了拓扑面 a,b,c,d,e 。对象B构成拓扑面c,f,i。拓扑面d 由 对象1,C构成。值得注意的是,拓扑面b由对象1,A构成;拓扑面h由对象4,D构成。可以看到,对象与拓扑面的关系为1:N;拓扑面与对象的关系为1:1或者 1:2 。原因同“输入数据”一节描述。
1)red,blue二元操作。
2)red,blue中同一层要素互相不压盖。
像在叠置分析(3):算法-对象模型到拓扑模型的关联 中的描述,建立对象模型与拓扑模型关联的方法是“标边”,即在弧段上记录label (由1到多个topolocation 构成)方法使得“线”代表“面”。
因此,与部分DCEL数据结构稍有区别,我们需要单独的Edge数据结构。其上聚合 label。有向边DirectedEdge的属性包含 Edge,bDirect(用于标识有向边是否与Edge同向),symEdge(对向边)。这种设计可以避免Label 被在双向DirectEdge上记录两次。
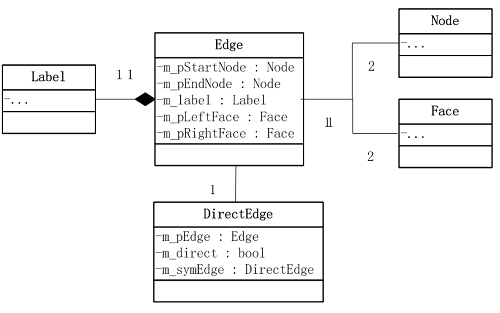
可以看到Edge不仅是建立对象模型与拓扑模型的桥梁,而且也是拓扑模型的核心。
3.拓扑面标记算法
为了求取两个图层的 交/并/差 集或者进行更广泛的 spatial join ,或者进行空间关系查询等叠置分析应用,需要对拓扑构建后的拓扑面进行标记。借助拓扑关系,我提出一种拓扑面标记方法,优点是不需要进行几何关系运算(相对于geos),效率非常高。
输入:构建了拓扑关系的拓扑(geos 称为geomgraph/planargraph ,CGAL称为DCEL,GIS平台中多以拓扑相称)数据,其中Edge上记录了Label信息。
输出:对于拓扑数据每个face,均标记其原始归属面id。因此Face上设置两个标记 red_id,blue_id ,缺省值为 -1。
算法思想:
1)建立数组 red[id] = edge* blue[id] = edge*;用于保存 与 red,blue图层每个要素关联的任意一个edge的指针。因为我们假设red,blue图层都是由多边形构成的,每个polygon仅含有一个联通区域 ,因此只需要记录任意一个edge的指针就够了。
2)对于每一个id,取出edge* ,查询label 中对应id内部(INTERIOR)的一侧(左侧或者右侧)并且取出这一侧的face,将red_id或blue_id 置为 id,放到 队列 queue中。
3)对每条边,根据 弧段 Edge 与 面Face 的关系,获得一个内部面后,向内进行“增长”,如果内部面邻接其他面的公共边不是内部面的边界,那么邻接面也是内部面,依次进行增长,直到增长到所有邻接的内部面。
while(!queue.empty())
{
Face* face = queue.front();
vector<DriectedEdge*> deEdges = face->getEdges();
for(int i=0;i<deEdges.size();++i)
{
DriectedEdge* deEdge = deEdges[i];
//如果deEdge代表id的边界,则不继续增长
if(deEdge->m_edge->m_label.get(id)[LEFT] == INTERIOR && deEdge->m_bDirect)
continue;
if(deEdge->m_edge->m_label.get(id)[RIGHT] == INTERIOR && !deEdge->m_bDirect)
continue;
//获取邻接面
Face* neighbourFace = deEdge.m_bDirect ? deEdge->m_edge->getRightFace():
deEdge->m_edge->LeftFace();
//根据实际情况,可能是red_id或者 blue_id
if(neighbourFace->red_id != id)
{
neighbourFace->red_id = id;
queue.push_back(neighbourFace);
}
}
queue.pop();
}
举例:
以对象1为例,含有对象1的label的Edge共有四段,可以从任意一段出发,比如从左上角一段出发,可以确定面a为内部面。标记a,并且加入队列中。
取队首a,对于a,的四条边,其中一条为1的边界面外,其他三个面为c,b,d,分别标记并加入队列。移除a。
取c的四条边,除一条为1的边界外,其他边邻接 a,b,e,因为 a,b已经标记,将e入队列。将c出队列。此时队列数据为 b,d,e。
取b的四条边,邻接面为a,c,d,均以标记。b出队列。
取d,没有新加入的内部面,d出队列。
取e,没有新加入的内部面,e出队列。对象1的标记结束,标记为1的面为a,b,c,d,e。
总结和对比:
采用内部面“增长”的方法充分利用了弧段-拓扑面的关系,发挥了拓扑数据模型的最大优势。对象模型的缺点就是查询对象间的拓扑关系需要实时计算得到,如果对于类似于空间分析这样需要反复大量查询拓扑关系的应用,不采用拓扑模型实现的效率是非常低下的。拓扑模型这样的数据结构建立后,面标记算法就是在数据结构基础上的算法,在这个算法的基础上,负责的地图叠置应用得以建立起来。
本节所描述的拓扑面标记算法,以及其他拓扑模型上的算法,是构建应用算法的基础。我认为应用算法,拓扑算法,拓扑模型三者的层次关系如下:

拓扑面标记算法是所有叠置算法必须实现的,对于geos,其采用了对象的边界对应的面确定一部分内部面,如对象1的边界邻接的 a,c,d,e面可以通过查询弧段直接得到,但是对于内部的面b却不是由拓扑面通过邻接关系增长出来的,而是通过了几何计算的方式确定b在A中,这样的效率就很低了,因为通过几何计算确定空间关系是比较耗时的。geos之所以采用这样的方法,也是因为 geos的拓扑模型没有 拓扑面的概念!因此拓扑面支持的操作就要用其他的方法来“绕路”了。
