拓扑(topology)是由DCEL构成的一种平面镶嵌数据结构。拓扑数据结构将平面划分为若干相互邻接且不压盖的拓扑面。在拓扑结构上实施的标记算法是叠置算法的核心(第四节)。这一节,我将介绍拓扑构建算法。
1.拓扑构建的总体流程
1.1 预处理
在面叠置分析算法中,输入数据为若干多边形(polygon)对象,这些多边形间的空间关系不定。预处理的任务是完成多边形到 Arc-Node 结构的转换。其中包含了线集求交、去重等算法环节,这两个环节完全工作在几何算法层面上(拓扑的构建大部分属于图的构建,相对几何算法复杂度低),算法复杂度较高,效率是实现的时候需要考虑的重中之重,因此需要合理安排处理流程,并且依据不同空间索引的优劣势配合使用。
叠置分析专题我计划从上至下,从应用至实现延伸,因此预处理的相关实现,我会在后期另行介绍,这里,我们需要了解的是预处理的输入及输出。
输入:
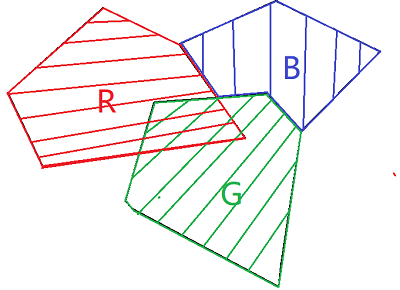
输出:
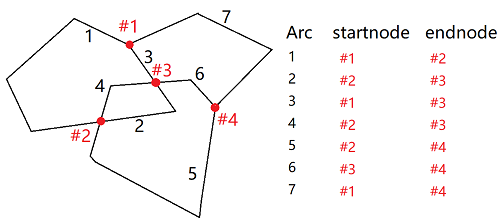
预处理的输出即拓扑构建的输入。
1.2 拓扑构建
拓扑构建的任务是在arc-node结构基础上,构建face。这些face可以保存邻接关系。在上一节中,我们看到,geos中是没有face结构的,因此不能够凭借graph结构查询边不存在交点的相交关系(如下图)。
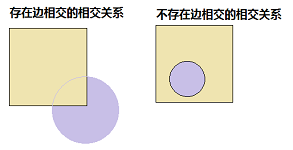
。geos采用几何计算的方式获得这样的关系,考虑到geos面向二元计算效率尚可以接受,而面向数据集的空间分析运算时,构建topo face就必不可少了。
拓扑构建的输出:
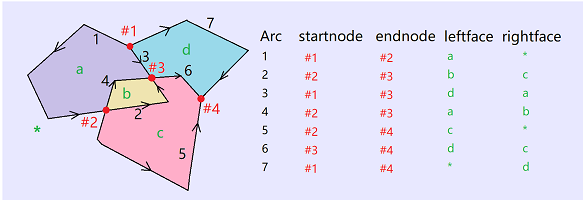
| 在geos中,存在两套功能类似的结构,一套按照业务名称称为geos::geomgraph ,一套按照定义称为geos::planargraph。geos中geometry的intersection,union,difference,spatial predict 等算法都是建立在geomgraph基础上的,而一些小的算法如 operation::polygonizer 等是构建在planargraph上的。我认为这两套结构可以均合并到geomgraph中。至于为什么做两套结构,我目前还没有理解清楚。 |
2.拓扑构建算法
拓扑构建算法可以分解为三个子步骤。
2.1 标记悬挂(dangle):
如果输入的数据均为多边形对象,那么标记悬挂这一步是没有必要执行的,因为不可能产生悬挂。但是考虑到多种不用不同的应用场景(比如geos中的利用一组折线构建多边形,或者利用输入的折线切割多边形),需要引入这一步。
所谓的悬挂边就是指任一端点度数等于1的弧段。标记悬挂,不能只将端点度数为1的线段标记出来,而是要“顺藤摸瓜”,将因为标记悬挂导致的更多的悬挂弧段标记出来。
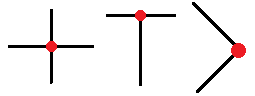
比如上图的情况,当从一个悬挂端开始标记,本来度数为2,3,4的节点关联的弧段也会被标记为悬挂。
| 节点的度数(degree)指节点关联的弧段的个数,当arc被标记为dangle时,不参与度数计算 |

被标记为悬挂的弧段不参与拓扑构面。
2.2 拓扑构面
拓扑面生成的法则是:下一弧段是当前弧段顺时针旋转后的第一条弧段。因此,拓扑构面需要对每个节点的出射有向弧段按照时针顺序进行排列。排序顺序可以为顺时针或者逆时针序。需要说明的是,排序依据的是每个有向弧段的前两个vertex构成的方向进行排序的,而不是整个弧段。
2.2.1 排序方法
比较简单的一种想法是根据方位角(航向)进行排序。因为反三角函数代价较大,有没有更高效的方式呢?一个想法是使用三角函数值,但是正弦、余弦在\([0,2\pi)\)范围上都不是单调的,正切更是还有值域的问题(无法表示\(\frac{1}{2}\pi\))。既然不能够在\([0,2\pi)\)上单调,可以将角度定义域划分为\([0,\pi),[\pi,2\pi)\)两部分呀。所以说 定义域划分+余弦/正弦是一种可行的方法。
还没有其他方式?还有一种思路是排序的时候只要给出两个元素的相对关系的定义,并且这样的关系满足传递率就可以了,在编程的时候对应所谓的仿函数。geos是怎么处理的?一是使用向量的相对位置关系:$$\vec v\times \vec v_1>0; \vec v_1在\vec v左侧 \\ \vec v\times\vec v_0<0 ;\vec v_0在\vec v右侧$$
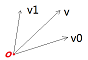
二是利用象限(Quadrant) 解决单调性的问题。象限在geos中多次被使用,在 geos::algorithm 命名空间中。后面提到单调链,仍然要利用象限。geos的象限顺序与中学数学中的象限定义一致。
综合一下,以逆时针排序为例:
- 如果\(Quadrant(\vec v_0)<Quadrant(\vec v_1) \) ,则\( \vec v_0<\vec v_1 \);
- 如果\(Quadrant(\vec v_0)>Quadrant(\vec v_1) \) ,则\( \vec v_0>\vec v_1 \);
- 否则若\( \vec v_0\times \vec v_1>0\);则\( \vec v_0<\vec v_1 \);
2.2.2 构面以及 cut edge的处理
拓扑构面的终止条件就是所有的 有向边全部遍历完毕。构建一个拓扑面的终止条件是边的闭合,即从一条边出发,顺时针旋转找下一条边,直至走完一圈,回到起点为止。伪代码如下:

依据上述代码运行,还会遇到一个问题,即有的边像“桥”一样将拓扑面切割。在geos中,这样的问题称之为cut-edge问题。见下图:
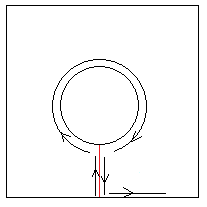
两种叫法都比较形象,按照上面的流程构建拓扑面,则在红色线上,面的两条边重合,这样不符合polygon的“simple”定义,因此,在构面时,这样的“桥”或者说“切割边”都需要被剔除。不幸的是,这样的边并不是悬挂,不能在一开始标记悬挂时被处理。
解决方案是,发现cut-edge时(它们的left-face与right-face相同),将它们标记为悬挂,从参与构面的弧段中剔除。剔除后,其所涉及到的边的关系需要更新。
2.2.3 外圈与洞的合并处理
完成2.2.2步骤后,我们会发现一个问题,由平面图构成的拓扑面是存在重叠的,比如下图中外圈左侧的面与内圈左侧的面其实应该是同一个面。因此,我们需要更新内圈的面,形象的说,就是给外圈”挖洞”。
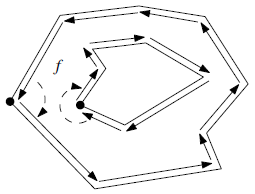
这个过程,需要使用内外圈的空间关系,因此也是需要几何运算的。任务可以描述为:针对每个内圈(顺时针圈,或洞),找到将其包围的最内侧内圈。两个问题需要解决。
1.如何判断拓扑面是逆时针顺序还是顺时针顺序。
判断多边形顺逆时针顺序的算法见博文 多边形面积以及顺逆时针顺序判断
2.如何搜索到包含内圈最内侧的外圈。
- 首先,取内圈最左侧点(x值最小的点)\(X\).
- 由\(X\)向左引射线,与相交的外圈计算出x值,保留\(X\)左侧的外圈。按照交点x值由大到小排序。
- 逐个对保留下的外圈判断点\(X\)是否在外圈内。找到的首个外圈为待求外圈。
- 如果找不到外圈,则证明此外圈为universe face的内圈。
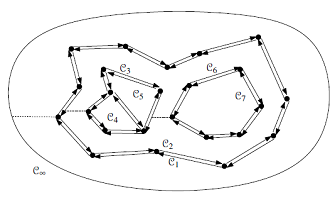
上图看对于内圈\(C_6\)其左侧的外圈分别为 \(C_5,C_4,C_2\) 其中\(X\)位于\(C_2\)中,因此,内圈\(C_6\)的外圈为\(C_2\) (图片来源:Berg M D, Cheong O, Kreveld M V, et al. Computational Geometry: Algorithms and Applications[M]. Springer Publishing Company, Incorporated, 2000.)
3.备注
- 本文的拓扑构建方法,在部分数据结构、部分算法方面均分别参考采纳了 geos 与 《computational geometry》(第三版,Berg等著)中的部分内容。但是整体方法、流程并不完全与以上两者相同。对上两者的处理方法感兴趣的读者请注意。
- 关于程序源代码。因为叠置分析涉及的算法比较多而且复杂,因此考虑单独建立工程分享至github。目前程序正在编写中,后期会统一更新代码地址。
